摘要
本文介绍了CPython中数据结构的关键操作的Big-O表示法。 big-o标记本质上是一种衡量操作时间复杂度的方法。 本文还说明了列表,集合和字典的许多常用操作。
为算法设计和选择正确的数据结构至关重要。
希望能帮助到你。
为什么我们需要知道时间复杂性?
对于数据科学家程序员而言,为工作选择正确的数据结构至关重要。 特别是,如果算法需要大量计算,例如训练机器学习模型的算法或处理大量数据的算法,那么确保选择合适的数据结构时要特别小心。
选择正确的数据类型通常会被忽略,并且最终会严重影响应用程序的性能。
文章目的
本文介绍了CPython中数据结构的关键操作的Big-O表示法。 big-O表示法是一种衡量操作时间复杂度的方法。
Python数据结构的时间复杂性
1.让我们了解大O符号的含义是什么?
在算法中执行许多操作。 这些操作可能包括遍历集合,复制项目或整个集合,将项目追加到集合中,在集合的开始或结尾处插入项目,删除项目或更新集合中的项目。
Big-O衡量算法运算的时间复杂度。 它测量算法计算所需运算所需的时间。 尽管我们也可以测量空间复杂度(算法占用多少空间),但本文将重点介绍时间复杂度。
用最简单的术语来说,Big O表示法是一种基于输入大小(称为n)来衡量操作性能的方法。
2. Big O表示法有何不同?
我们需要熟悉许多常见的Big O符号。
让我们考虑n为输入集合的大小。 就时间复杂度而言:
O(1):无论您的集合有多大,执行操作所花费的时间都是恒定的。 这是恒定的时间复杂度符号。 这些操作尽可能快。 例如,检查集合内部是否有任何项目的操作是O(1)操作。
O(log n):当集合的大小增加时,执行操作所花费的时间对数增加。 这是对数时间复杂度表示法。 潜在优化的搜索算法为O(log n)。
O(n):执行操作所需的时间与集合中的项目数成线性正比。 这是线性时间复杂度符号。 就性能而言,这介于两者之间或中等。 作为一个实例,如果我们想对一个集合中的所有项目求和,那么我们将不得不遍历该集合。 因此,集合的迭代是O(n)操作。
(n log n):执行某项操作的性能是集合中项目数量的拟线性函数。 这称为准线性时间复杂度表示法。 优化排序算法的时间复杂度通常为n(log n)。
O(n平方):执行操作所需的时间与集合中项目的平方成正比。 这称为二次时间复杂度表示法。
(n!):当在操作中计算集合的每个单个排列时,因此执行操作所需的时间取决于集合中项目的大小。 这称为阶乘时间复杂度表示法。 非常慢。
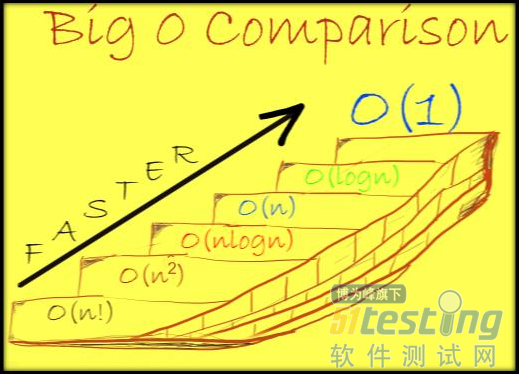
该图像概述了Big-O符号。
O(1)很快。 O(n平方)很慢。 O(n!)非常慢。
大O符号是相对的。 大O表示法与机器无关,忽略常量,并且被包括数学家,技术人员,数据科学家等在内的广泛读者所理解。
最佳,平均,最差情况
当我们计算操作的时间复杂度时,我们可以根据最佳,平均或最坏情况产生复杂度。
最佳情况方案:顾名思义,这是当数据结构和集合中的项目以及参数处于最佳状态时的方案。 例如,假设我们要在集合中找到一个项目。 如果该项目恰好是集合的第一项,那么这是该操作的最佳情况。
平均情况是根据输入值的分布定义复杂度。
最坏的情况是可能需要一种操作,该操作需要在大型集合(例如列表)中找到位于最后一个项目的项目,并且算法会从第一个项目开始对集合进行迭代。
Python集合和时间复杂度
在本文的这一部分中,我将记录CPython中的常见集合,然后概述它们的时间复杂性。
我将特别关注平均情况。
1.List
List是迄今为止Python中最重要的数据结构之一。 我们可以将列表用作堆栈(添加的最后一项是第一项)或队列(添加的第一项是第一项)。 列表是有序且可变的集合,因为我们可以随意更新项目。
让我们回顾一下常见列表操作及其Big-O表示法
插入:Big-O表示法是O(n)
获取项目:Big-O表示法为O(1)
删除项目:Big-O表示法是O(n)
迭代:Big-O表示法是O(n)
获得长度:Big-O表示法为O(1)
Joshua Sortino在Unsplash上拍摄的照片
2.Set
集合也是Python中使用最广泛的数据集合之一。 集合本质上是无序集合。 集合不允许重复,因此集合中的每个项目都是唯一的。 集合支持许多数学运算,例如联合,差,集合的交集等。
让我们回顾一下通用Set操作
检查集合中的项目:Big-O表示法是O(1)
集合A与集合B的区别:大O表示法是O(A的长度)
集A和B的交集:大O表示法是O(A或B的长度的最小值)
集A和B的并集:相对于长度(A)+长度(B),它的Big-O表示法是O(N)
fabio在Unsplash上的照片
3.Dict 字典
最后,我想提供字典数据收集的概述。 字典是键值对集合。 键在字典中是唯一的,以防止项目冲突。 这是非常有用的数据收集。
字典由键索引,其中键可以是字符串,数字甚至是带有字符串,数字或元组的元组。
我们可以对字典执行许多操作,例如存储键的值,或基于键检索项目,或遍历项目等。
让我们回顾一下常见的词典时间复杂度:
在这里,我们认为该密钥用于获取,设置或删除项目。
获取项目:Big-O表示法为O(1)
设定项目:Big-O表示法是O(1)
删除项目:Big-O表示法是O(1)
遍历字典:Big-O表示法是O(n)
NASA在Unsplash上拍摄的照片
本文内容不用于商业目的,如涉及知识产权问题,请权利人联系博为峰小编(021-64471599-8017),我们将立即处理